I mentioned in a recent edit that I rather enjoyed Aug 22’s numerical Listener crossword. As most people hitting these pages will know, The Listener Crossword appears each week opposite the Times Jumbo Cryptic. The numeric crosswords appear every three months and are a bit of a love/hate thing for Listener fans. I rather like them and, having not done one for a while, I thought I’d give it a go.
Now that the deadline has passed for submissions, I thought as a one-off post I’d stick the solution on here, purely because the message in the grid made me laugh.
The idea of this puzzle was to determine the values, 1-19, of the letters used in 39 algebraic equations forming the across and down clues. We are told that three of the solutions are palindromes, 8d, 24d and 29d. The solutions were then to be slotted into the grid with each cell containing one or two digits. The values in each cell were then to be replaced by their equivalent letters.
You were given the following grid and clues:
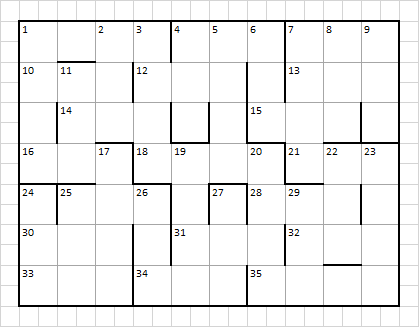
Across clues
1. (MAR)C+H (5)
4. COM(E+T) (4)
7. TRIT+O-N (4)
10. CO(M+B)+A+T+S (3)
12. DA(M+E) (4)
13. ROU-T (4)
14. A(NG+S)+T! (4)
15. VIV+A+S (4)
16. INC(U-R+S+I+O+N)+S (4)
18. BANT(E+R-S)-M+E+T (5)
21. TA+RR+IE+R-S (4)
25. G+O-I+N-G+B+A+NA+N(A+S) (4)
28. A(KA+V)A (3)
30. W(A-S)-O+K (3)
31. A(I+D)+E! (3)
32. COOL-S (4)
33. B(O-B)SL+E(I-G)+HT+EA+M (6)
34. NIN+E-S (3)
35. MALT (4)
Down clues
1. BBILB+(O+B)(A+G)-GI+N+S (5)
2. WAR(L-O+C+K) (4)
3. RA-T+(E+N-T+E-R+S)A(BIN-N) (6)
4. T-O+T+AI-WAN (4)
5. U-S-E+B(E-A)N+TI(N+S) (4)
6. L(E-C)+(T+U+R(E+R)+O/O)M (5)
7. M(A-G-N+E+TI+S)M (5)
8. GL(OB+U-L-E) (4)
9. MARACA+S (4)
11. TALL-M+E-N (4)
17. CAR+N(I+V+A(L+S)) (5)
19. VERV+E-S (4)
20. WRIN+K-L+E+S (4)
22. (R-A)BA-T (4)
23. BANN+TV (5)
24. L(U+M+BE+R+S) (4)
25. MO(O+D) (4)
26. (L+O+G)IC (4)
27. CE(R-A+M+I+C)-S (4)
29. TA (3)
As ever with these things, half the battle is in finding an entry point into the equations. On this occasion, the entry point was relatively easy. The clue for 29d is TA, a 3-digit number. We know from the preamble that 29d is a palindrome. Only two 3-digit numbers fit the bill: 112 = 121, and 73 = 343. Another clue, 14a, A(NG+S)+T!, a 4-digit number, allows us to narrow in on the values of T and A. If T was 11, then T! or 11x10x9x8x7x6x5x4x3x2x1 would be 39,916,800 – much too big. 7! on the other hand, or 7x6x5x4x3x2x1 is 5040. Therefore T=7 and A=3. 29d is therefore 73 = 343. 14a then becomes 3(NG+S)+5040.
From then on it’s a case of keeping track of each equation, slotting in the values of the letters as you deduce them. Adding the solutions you’ve deduced to the grid where possible also helps.
The equations featuring powers or factorials are key as they help eliminate potential values for each letter. For example, 21a, TA+RR+IE+R-S, a 4-digit number, suggests R is no more than 5 because 66 is 46,656 and S could never be enough to bring that down to 4 digits.
Certain clues featuring powers are doubly key as they help to further narrow possible ranges for certain values. For instance, 30a, W(A-S)-O+K, tells us that S is going to be less than A. This is because negative powers yield decimal values less than 1, which you would not be able to fit into the grid. As we’ve deduced A to be 3, this suggests S is going to be either 1 or 2. In this case, S=1 because no value of W(3-2) can yield enough for the solution to be a 3-digit number.
A number of clues let us narrow in on values for C, R and E.
5d, which is now U-1-E+B(E-3)N+7I(N+1), and 31a, 3(I+D)+E!, allow us narrow in on a value for E. 5d tells us that E is going to be more than 3 thanks to the power (E-3), while 31a tells us that E is going to be 6 or less due the solution being a 3-digit number (6! being 720 – anything larger and you’ll bust). E is therefore going to be 4, 5 or 6.
The power (E-C) in 6d, which is now L(E-C)+(8+U+R(E+R))M, tells us that C is going to be less than E. C is therefore going to be 2, 4 or 5. (We’ve already established S=1 and A=3.)
17d is now C3R+N(I+V+3(L+1)), a 5-digit number. With C being a minimum of 2, R cannot be more than 5. (23×5 = 215 = 32,768, while 23×6 = 218 = 262,144 – too big.). R is therefore going to be 2, 4 or 5.
21a is now 20+RR+IE+R, a 4-digit number. The maximum IE can be at this point is 18×19=342. 22=4 and 44=256 aren’t going to be enough to make a 4-digit solution, but 55 =3125. Therefore R=5.
Going back to 17d, now C15+N(I+V+3(L+1)), we now see that C=2 for the solution to remain a 5-digit number. If C was 3, C15 would be 14,348,907 – too big.
27d is now 2E(4+M+I)-1, a 4-digit number. With 1, 2, 3 and 5 now spoken for, E must be either 4 or 6. The most (4+M+I) can be at this point is (4+18+19) = 41. If E was 4, this would be 24*41-1=655, which is too small. Therefore E=6.
By now we’ve established which letters represent 1, 2, 3, 5, 6 and 7. Powers continue to play a crucial part in deducing further values.
4d is now 14-O+3I-3WN, a 4-digit number. The least 3WN is going to be at this point is 3x4x8=96. We can therefore see that 3I is going to form the lion’s share of this number. I=4 is too little, as 34=81. I=9 is too much, as 39=19,683. (The most 3WN can be to reduce this is 3x18x19=1026.) Therefore I=8.
33a is now B(O-B)L+6(8-G)+7H+18+M, a 6-digit number. The power (8-G) tells us that G is going to be less than 8. As 1, 2, 3, 5, 6 and 7 are already spoken for, G=4.
25a is now O-5+N+B+N3+N4, a 4-digit number. Numbers 1-8 are now deduced. If N was 10, then 25a would be O-5+10+B+1000+10000 – too big for a 4-digit number. Therefore N=9.
By now you’ll have solutions for some clues that can be slotted into the grid, allowing you to deduce further values.
14a is 5151, 21a is 3198, 34a is 653 and 29d is 343. As we know the numbers in the grid are to be swapped for letters, this means two-digit cells are going to be a maximum of 19. The solutions will therefore be entered into the grid as 5-15-1, 3-19-8, 6-5-3 and 3-4-3 respectively. Also, 7a at the moment is 1951+O, so, with numbers 1-9 already deduced, this will eventually be a value between 1961-1969. (7a can’t be 1970 as 9d cannot begin with a 0.) We can therefore also fill in the first two cells of 7a, i.e. 19-6-(?).
(Additionally, we know that 8d is a palindrome, 4-digits, 3 cells long, now beginning with 6. It must therefore end with a 6. We know only values 1-19 can be entered into each cell. The solution for 8d can only therefore be 6116, entered either as 6-11-6 or 6-1-16.)
At this point, the grid will look like this:

Doesn’t seem like much, but believe it or not we’re near the end!
7d is now 53M2, a 5-digit number. We can see from the grid that it begins with 19 and ends with 3. The only value that fits is M=19, making 7d 19133 (entered as 19-1-3-3).
A couple more solutions now drop into place. 9d is 5131 (entered as 5-13-1) and 27d is 1983 (entered as 19-8-3).
By virtue of solving 9d we now know the solution to 7a is 1965. The clue at the moment is 1951+O, which means O=14.
22d is now 2B3-7, a 4-digit number beginning with 19. Therefore B=10, making 22d 1993 (entered as 19-9-3).
More solutions drop into place. 4a is 6916 (entered as 6-9-16), 10a is 823 (entered as 8-2-3), 18a is 18894 (entered as 18-8-9-4), 25a is 7318 (entered as 7-3-18) and 3d is 711118 (entered as 7-11-1-18 due to 14a ending in 1).
The grid is now taking shape:

Next, we think back to 8d, which we know will be 6116, entered as 6-11-6 or 6-1-16. We’re told that 13a, crossing 8d midway, will be a 4-digit number squeezed into 3 cells. The first and last two digits of 13a have been solved, meaning that the remaining digit is single. 8d, which crosses 13a, must therefore be written in as 6-1-16. This means 13a is 1113. With the clue for 13a being 70U-7 at the moment, this means U=16.
Further solutions drop into the grid as a result. 16a is 6193 (entered as 6-19-3) and 5d is 9569 (entered as 9-5-6-9).
15a is now 8V2+4, a 4-digit number we now know will end in 316. Therefore V=17, making 15a 2316 (entered as 2-3-16).
Further solutions drop into the grid as a a result. 19d is 8675 (entered as 8-6-7-5) and 23d is 81119 (entered as 8-1-11-9 – this is because 32a is 4 digits crammed into 3 cells, and we already know the first two cells of 32a are 4 and 3).
6d is now L4+1501, a 5-digit number we now know will begin with 16 and end with 2. Therefore L=11, making 6d 16142 (entered as 16-14-2).
A ton of solutions now drop into the grid as a result. 32a is 4311 (entered as 4-3-11 – already solved by virtue of solving 23d), 35a is 4389 (entered as 4-3-8-9), 1d is 88146 (entered as 8-8-14-6), 8d is 6116 (entered as 6-1-16 – already completed when deducing U), 11d is 2519 (entered as 2-5-19 – already filled in by other solutions), 17d is 33317 (entered as 3-3-3-17), 24d is 1111 (entered as 1-1-11 – this is because 33a is a 6-digit solution crammed into 3 cells, so all three cells will be values 10-19) and 26d is 1856 (entered as 18-5-6).
12a is now 75D, a 4-digit number we now know will begin with 11 and end with 5. Therefore D=15, making 12a 1125.
Further solutions drop into the grid as a result. 31a is 789 (entered as 7-8-9) and 25d is 7714 (entered as 7-7-14).
4d is now 6561-27W, a 4-digit number we now know will begin with 62. The last two digits are entered into a single cell, meaning they are 10-19. Of the undetermined values remaining (12, 13 and 18), only W=13 results in a solution ending this way, making 4d 6210.
20d is now 4676+K, a 4-digit number we now know will begin with 4 and end with 94. Therefore K=18, making 20d 4694 (entered as 4-6-9-4).
Further solutions drop into the grid. 28a is 639 (entered as 6-3-9 – already in the grid thanks to other solutions), 30a is 173 (entered as 1-7-3 – ditto) and 2d is 3315 (entered as 3-3-15).
Finally, H must be 12 as it’s the only value left. This drops in 1a, 81237 (entered as 8-12-3-7).
The completed grid therefore looks like this:

Which, when replaced with their letter equivalents, spells out the following message:

In all, a great puzzle! If you are reading this, Piccadilly, 10/10. Great construction, witty solution and good progression throughout. Loved it.
Laters,
LP
Thanks for that. I never understood how they worked. May try the next one!
Cool, cool! I hope the next one is as good. – LP
This is brilliant. We’d never noticed that puzzle before, but it’s proper maths and very cleverly put together. We made a start but soon lost our way, so your analysis was really helpful.
Please could you do this again for the next one?
Thanks!
Glad you liked the post. I dread to think how long it took Piccadilly to come up with all the clues, but I agree, it was an excellent puzzle. If I crack the next one, I’ll write it up once the submissions deadline has passed. – LP